Haskell で RealTimeQueue
@autotaker1984 さんの以下の記事について考えました。
永続リアルタイムキューのHaskell実装と計算量解析 - autotaker's blog
head / tail するときに、reverse さえ完了していれば問題ない、だから snoc で停止計算を進行させる必要はない、というのはなんとなく説得力があります。
けれども PFDS では、 rotate が始まるときに停止計算がすべて完了していること(負債を完済していること)にこだわっていました。
それは、停止計算が重なると再帰的な呼び出しで計算量が増えるからです。
たとえば空のキューに 1 から 15 まで snoc すると、frontList は以下のような状態で、go 関数の呼び出しが再帰的になります。
go [] (go [] (go [] (go [] [] [1]) [3, 2]) [7, 6, 5, 4]) [15, 14 .. 8]
ここから tail すると以下のように 4 ステップかかります。
go [] (go [] (go [] (go [] [] [1]) [3, 2]) [7, 6, 5, 4]) [15, 14 .. 8] => go [] (go [] (go [] (1 : []) [3, 2]) [7, 6, 5, 4]) [15, 14 .. 8] => go [] (go [] (1 : go [3] [] [2]) [7, 6, 5, 4]) [15, 14 .. 8] => go [] (1 : go [7] (go [3] [] [2]) [6, 5, 4]) [15, 14 .. 8] => 1 : go [15] (go [7] (go [3] [] [2]) [6, 5, 4]) [14, 13 .. 8]
さらに tail する場合も以下のように 3 ステップかかります。
go [15] (go [7] (go [3] [] [2]) [6, 5, 4]) [14, 13 .. 8] => go [15] (go [7] (2 : [3]) [6, 5, 4]) [14, 13 .. 8] => go [15] (2 : go [6, 7] [3] [5, 4]) [14, 13 .. 8] => 2 : go [14, 15] (go [6, 7] [3] [5, 4]) [13, 12 .. 8]
ざっくり言うと O(1) ではなく O(log(n)) かかってしまうように思います。
世界一短い自己紹介
R 教授による S 大学での講義録。
はじめに
かねてから話していたとおり、今回はクワインについて講義する。
そもそもクワインとは何か?自分自身と同一の文字列を出力するプログラムのことである。自己言及のパラドックスに絡めて語られることもあるが、あくまでも、自身の「表現」つまり文字列を出力するだけなので、プログラマの諸君はそれほど混乱することもないだろう。
コンビネータ計算でクワインというと、以前に fumi 氏が記事を書いている。基本的な考え方はそこに書かれている通りである。
まず「関数の表現」を得るために、「関数」を何らかの方法でコード化(符号化)する。この「コード」を入力として「関数の表現」と「コードの表現」を出力できれば、関数(コード)= 関数の表現 ++ コードの表現 ≒ 関数(コード)の表現、となりクワインの完成である。
符号化その1(16161)
fumi 氏はチャーチ数のリストによって符号化を実現としている。たとえば、`sk という「関数」であれば、[0, 1, 2] = ``s``si`k`sk`k ... `kk という「コード」になる。この場合、入力した「コード」をもとに、「関数の表現」である [96, 115, 107] というチャーチ数のリストと、「コードの表現」である [96,96,115,96,96, ... ,96,107,107] というリストを構築できればよい。
この方針で fumi 氏は 25677 bytes のプログラムを得た。
さらに以下のような手法を適用することで、16000 bytes 程度まで短縮できることを確認している。
- 「コード」を表すために 0 から 3 までのチャーチ数を利用しているが、以前に解説した 51b 数をさらに false = SK の関数と捉えることにより、それぞれ 0 = K, 1 = I, 2 = SS, 3 = S(K(SS))(SS) という関数に置き換える。
- `, i, k, s を表す 96, 105, 107, 115 というチャーチ数を 96 + f 9 と捉え、それぞれ λx. 0, λx. x, λx. x+2, λx. x+(x+1) といった関数に置き換える。
- 文字列を連結する (++) などの関数は、何度も使うので共通化する。
ここでボトルネックとなるのが、リストである。リストに要素を一つ追加するごとに cons x y = ``s``si`kx`ky として 10 文字程度のオーバーヘッドが発生してしまうため、リストを使うと「コード」のサイズが大きくなり、最終的には本体の「関数」の 10 倍以上の長さとなってしまうのだ。
そこでリストを使わずに「コード」を表現することを考える。
符号化その2(2792)
実は Lazy K の処理系に、2792 bytes のクワインのプログラムが付いている。このプログラムには基となる scheme のプログラムが付属していないため、Lazy K のプログラムそのものを解析する必要がある。仕方がないので、心眼や第6感を駆使してプログラムを読み進めると、このプログラムではどうやら、`, s, k それぞれが s, ks, kk という「コード」として符号化されていることに気付く。
Lazy K の Unlambda 記法では適用演算子 ` がプログラムの約半分を占める。したがって、` に 1 文字、k と s に 2 文字を割り当てる符号化は「コード」の短縮に有効だと考えられる。
さらに「コード」を「関数」に与える際、リストにせず複数の引数を直接与えている。これは「コード」のサイズを抑えるうえで極めて有効である。ただし、再帰を止めるために、「コード」の終了を検知する仕組みが必要となる。
もっと短く(1283)
さらに簡潔なプログラムを得るためには、どのような手法が考えられるだろうか。
私は以下の手法を採用した。
チャーチ数による再帰
前回解説したチャーチ数による再帰が、クワインでも有効である。
これにより終了判定が不要となり全体的に短くなるが、決められたチャーチ数に合わせて引数の数を調整することが必要となる。
たとえば今回は 512 (2^9) 回再帰することにしたが、そのためにプログラム先頭の適用演算子 '`' の数を調整している。
差分リスト
与えられたコードからプログラムの表現とコードの表現を再現するわけだが、それらの文字列=リストを作ってしまうと、ほしい結果を得るためには、リストを逆順にしたり連結したりする必要があり、プログラムが大きくなってしまう。これを避けるためには、途中結果を差分リスト≒継続の形で持つのがよい。
そうすれば、引数が与えられる度に継続を合成して最後に適用するだけで、望みどおりの結果を得ることができる。
たとえば A, B, C というコードから"abcCBA"という表現を得る方法は、それぞれ以下のようになる。
(簡単のため、引数のコードは逆順で与えるものとする)
リストの場合
-- 途中結果を (プログラムの表現, コードの表現) という形で持つ f ("" , "") C B A => f ("c", "C") B A => f ("bc", "BC") A => f ("abc", "ABC") -- コードの表現を逆順にしてプログラムの表現と連結する => "abcCBA"
差分リストの場合
-- 途中結果を差分リストの形で持つ f id C B A => f (('c':).id.('C':)) B A => f (('b':).('c':).id.('C':).('B':)) A => f (('a':).('b':).('c':).id.('C':).('B':).('A':)) -- 引数の差分リストを "" に適用するだけでいい => "abcCBA"
SKから真偽値への変換
引数が S であるか K であるかによって場合分けが必要となる。私は以下のような関数を定義した。
sk2bool K = K = True, sk2bool S = S K = False となり、条件分岐が実現できる。
sk2bool x = S S S x (S K x) K
関数の構成
これまでのテクニックを踏まえて具体的な関数を構成する訳だが、引数の型や順序、ロジックの共通化など、どう構成すれば簡潔になるかという明確な指針は得られていない。私は以下のように定義した。
-- f は自分自身、k は差分リスト、x と y は引数で与えられたコード quine f k x y = if sk2bool x then f (('`':) . k . g x) y else f (g y . k . g x . g y) where g x = if sk2bool x then ('K':) else ('S':)
abstraction elimination の振る舞いをどれだけ具体的に想像できるかが、短縮の鍵である。
おわりに
これらの手法を採用したことより、1283 bytes のクワインが得られた。
短くなったとはいえ、1000 bytes を超えるサイズである。さらなる短縮の可能性はまだあるのではないだろうか。諸君の積極的な挑戦を期待している。
Hello, world! ふたたび
R 教授による S 大学での講義録。
はじめに
えー、前回の講義からだいぶ間が空いてしまったが、講義を始めたい。
今回はクワインについて話す予定であったが、その前にもう一度だけ Hello, world! について話をさせてほしい。
前回の講義の直後、irori 氏によって、399bytes の Hello, world! の存在が証明された。
その詳細について氏は何も語らなかったが、今年の 7 月になってソースコードが公開された。
それを解読した結果、および解読の過程で新たに得られた知見について、今回の講義では話をしたいと思う。
ロジックの見直し(451)
前回の講義で "Hello, world!" という文字列に対応するチャーチ数を得るため、
<27> + f <73> <81>
という式を提示した。だが、どうやらこれは少々複雑に過ぎるようである。
<28> + f <80>
という式の方が、必要なチャーチ数を簡潔に生成できることが分かっている。
Jot 記法(421)
irori 氏のコードを読むと、'0' という見慣れない文字が頻繁に出てくることに気づく。
これは何か?そう、Jot 記法である。
Lazy K で Jot 記法は以下のように定義されている。
NonemptyJotExpr
::= JotExpr "0" (JotExpr S K)
| JotExpr "1" (lambda (x y) (JotExpr (x y)))つまり単体の 0 は SK すなわち真偽値の「偽」と等価である。
SK は 51b 数にも必ず登場するため、"`SK" を "0" に置換することでコードを大きく短縮できるのだ。
irori 氏の手法(399)
irori 氏は、さらに以下の 3 つの手法を用いてコードを短縮し、400bytes を切るまでに至った。
関数の構造の見直し
もともと私が定義していた関数の構造は以下のとおりである。
hello a x = if x == 0 then a else hello (g x : a)
これに対して irori 氏が定義した関数の構造は以下のようになっている。
hello a x = (if x = 0 then tail else hello) (g x : a)
追加された tail の分、操作は増えているが、引数 a の出現箇所が減っているので、abstraction elimination 時のコード増加量が抑えられ、結果的に 15bytes ほど短くなっている。
51b 数の有効活用
51b 数はチャーチ数を生成するためのものであり、チャーチ数に変換してから、すなわち B コンビネータを与えてから利用するというのが本来の使い方である。
だが、51b 数に他の値を与えることにも意味がある。irori 氏は SK を与えることで、再帰の終了判定を簡潔に記述しており、5bytes ほど短くなっている。
さすが 51b 数の生みの親である。51b 数を深く理解されている。
ちなみに 51b 数
<N> f x => (f x (f x (f x ... (fをN-1回適用) ... (f x x)))))
チャーチ数による再帰(365)
300bytes 台を達成したところで、これ以上の短縮は不可能であろうか?
いや、キリのよいサイズのコードはまだ縮むというのがゴルファーの間の鉄則だ。これはむしろ、より短いコードへの足掛かりと捉えるべきである。
これまでのコードをさらに短縮する上では、やはり関数の構造に大きく手を入れることが不可欠であろう。
また irori 氏は 51b 数を有効に活用していたが、他にも同じようなことができないだろうか。
ここまで考えて私は、Hello, world! のメインループを書き換える方法に思い至った。
明示的に再帰構造を記述するのではなく、チャーチ数により再帰を実現するのである。
どういうことか?たとえばチャーチ数 <3> が与えられたとき、
f a b x = a (x : b)
のように定義しておくと、<3> f a b x y z という式は以下のように簡約され、f を再帰的に 3 回呼ぶのと同じ効果が得られる。
<3> f a b x y z => f (f (f a)) b x y z => f (f a) (x : b) y z => f a (y : x : b)) z => a (z : y : x : b)))
固定長の引数を扱うプログラムでは、再帰を終了させるための条件分岐も不要になり、コードを大きく短縮することが可能である。
今回の場合、これにより 365bytes のコードを得ることができた。
実はこの手法(チャーチ数による再帰)は関数型プログラマの間では比較的ポピュラーなものであり、Grass におけるショートコーディングなどでも活用されている。今回、私が気づかなかったのは、ひとえに私の力不足によるものである。
おわりに
というわけで、Hello, world! における irori 氏の手法と、新たに得られた知見について解説した。
次回の講義では、今度こそクワインについて話すつもりだ。
究極の関数型言語による至高のHello, world!
以下の記事は、 R 教授による S 大学での講義録を Haskell Advent Calendar 2012 のために転載したものである。
はじめに
えー、それでは、今年最後の授業を始めたいと思う。今日は『究極の関数型言語による至高の Hello, world!』について講義することにしたい。
“究極”の関数型言語が何であるかについては諸説あろうが、ここでは SKI コンビネータ計算を指すものとする。また“至高”の定義を、最も簡潔であること、すなわち最も短く記述されていることと定める。
諸君は第一プログラミング言語として Haskell を選択している者がほとんどであろう。当初この講義も Haskell をベースに行おうと考えていた。だが、Haskell は非常に巨大な言語となってしまっており、言語仕様を把握するだけでも難しい。だいたい STG が Spineless Tagless G-machine だろうが、Shared Term Graph だろうが、違いの分かる者がどれだけいるだろうか。また最近の Haskell は、HTTP という世俗的な目的のためにフレームワークを用意するなど、大衆に媚びておる。ここは純粋関数型言語の原点に立ち返ることが必要であろう。
いずれにせよ、Haskell を含めた純粋関数型言語を深く理解する上で、コンビネータ計算/論理は極めて重要な概念である。コンビネータ計算に習熟すれば、遅延評価もポイントフリースタイルも思いのままなのである。なお一点だけ断っておくと、コンビネータ計算の世界に型はない。プログラミングを誤るとデバッグは極めて困難である。だが世の中、Haskell のように素晴らしい型を持つ言語ばかりではない。諸君も必要に迫られて Ruby や Perl を触らなくてはならないときがあるかもしれない。そんなときのためにも、型に頼らずバグを見つける嗅覚を養っておくことは重要であろう。
なおコンビネータ計算を具現化した言語として、今回は Lazy K を採用する。より簡潔なプログラミングを志向する者が集う場も提供されているので、諸君もこの講義を機に、ぜひ参加するとよいだろう。なに?Haskell Golf は止めたのかだと?Haskell Golf では henkma 氏に勝てないので 研究が忙しくてな、今は休んでおる。
チャーチ数とリスト(15620)
さて本題に入ろう。
"Hello, world!" という文字列を出力することが、プログラムの目的である。関数型言語において、文字列は文字のリストに決まっている。配列を使おうなどという考えは堕落である。また Lazy K において、文字はすなわちチャーチ数なので、チャーチ数のリストを得るというのが最初の目標となる。
念のため確認しておこう。チャーチ数は 0 = λ f x . x, 1 = λ f x . f x, 2 = λ f x . f (f x) となるような関数のことだ。SKI で表現すると、0 = SK, 1 = I, 2 = S(S(KS)K)I 。B = S(KS)K とおけば 2 = SBI となり、さらに任意のチャーチ数 n について n = SB(n-1) として帰納的に導ける。なお 0 = KI と表現する方が一般的かもしれないが、SK の方が何かと都合がよいので、今後はこちらを用いる。
また Lazy K におけるリストは cons = λ x y z . z x y という関数である。car = K, cdr = SK とおくと、(cons x y) car = Kxy = x, (cons x y) cdr = SKxy = y となり、リストとして機能していることが容易に確認できる。変数 z を除くと cons x y = S(SI(Kx))(Ky) となる。出力リストの終わり end-of-output は λ z . 256 = K 256 である。
これだけの知識があれば、以下のように仕様を満たすプログラムを書くことができる。
K(cons 72 (cons 101 (cons 108 (cons 108 ( ... (cons 33 end-of-output))))))
ここで 72('H')は、実際には SB(SB(SB( ... (72回適用) ... I))) = S(S(KS)K)(S(S(KS)K)(S(S(KS)K))(...I))) という記述になる。その他の数も同様である。
また Lazy K では入力がプログラムの引数として渡されるので、それを無視するため、先頭に K を置いている。
このプログラムは正しく動作するが、美しいとは言いがたい。何しろ 15620 bytes にもなるのだ。
いかにしてこれを簡潔に記述するかというのが、今日のテーマである。
算数(974)
Lazy K の処理系をここから取得しているなら、lazier.scm というファイルが含まれているだろう。これは scheme で書かれた DSL から Lazy K プログラムを生成するコンパイラであるが、これを利用して Hello, world! プログラムを生成してみよう。以下のような scheme プログラムを実行してみる。
(load "lazier.scm") (load "prelude.scm") (load "prelude-numbers.scm") (lazy-def '(hello input) '(cons 72 (cons 101 (cons 108 (cons 108 (cons 111 (cons 44 (cons 32 (cons 119 (cons 111 (cons 114 (cons 108 (cons 100 (cons 33 end-of-output)))))))))))))) (print-as-cc (laze 'hello))
これで生成されるプログラムは 1050 bytes。さらに最後の行の print-as-cc を print-as-unlambda と書き換えて Unlambda 記法で出力するようにすれば、974 bytes まで縮む。先ほどのコードのなんと 1/16 である。
何が違うのか具体的に見てみよう。
まず cons については特に変わりない。S(SI(Kx))(Ky) という表現が随所に出てくることが確認できる。
変わったのは、個々のチャーチ数である。たとえば 72('H') は S(K(SII(S(S(KS)K)I)))(S(S(KS)K)(S(S(KS)K)(S(SII)I(S(S(KS)K)I)))) と表現されている。
これがどのように導出されたかは、prelude.scm と prelude-numbers.scm を確認すれば分かる。関連する箇所を抜粋すると以下のようになっている。
72 = 4 * 18 18 = (1 +) 17 17 = (1 +) 16 16 = (λ x . x x x) 2 4 = (λ x . x x) 2
(1 +) は先ほど説明した SB = S(S(KS)K) である。
(*) の定義は λ a b f . a (b f) となっている。これが実際に a * b と等価であること、さらに S(Ka)b と書けることは、各自で確認してほしい。
16 と 4 の定義にあるラムダ式を理解するには、チャーチ数におけるべき乗が x ^ y = λ y x . y x となることを理解しておく必要がある。すなわち、λ x . x x は x ^ x、λ x . x x x は (x ^ x) ^ x と等しく、引数に 2 を与えれば、それぞれ 4 と 16 が得られる。
なお、λ x . x x = SII, λ x . x x x = S(SII)I である。ラムダ式から SKI コンビネータへの変換(abstraction elimination)については、資料もあるし、最終的にはプログラムに実行させることになるだろう。だが、これを十分に理解しておくことが、SKI コンビネータを自在に操れるようになるための鍵である。紙と鉛筆による演習をお奨めする。
さらに算数(687)
チャーチ数をこれ以上簡潔に記述することは不可能だろうか?いや、そんなことはない。先ほど例に挙げた 72('H') には B = S(KS)K が 4 回も出現する。これをまとめれば、より短い記述ができそうである。このことにいち早く気付いたのが 51b 氏である。氏はチャーチ数を B の関数とみなすことにより、それぞれのチャーチ数がどのように記述されるか整理した。このようにチャーチ数を B コンビネータの関数とみなし、B を除去したものを 51b 数と呼ぼう。
51b 数に関する代表的な演算の規則を、以下にまとめる。51b 氏オリジナルの規則に加えて、私が気付いたものもいくつか加えている。
(1 +) が SS と 2 項で書けること、(1 + xB) ^ xB や (1 + xB) * xB がもとの xB に加えてたった 4 項の追加で実現できることなどがコードの短縮に大きく寄与している。
1 + xB = SB(xB) = SSxB xB + yB = xB(SB)(yB) = S(SxS)yB xB * yB = B(xB)(yB) = S(SIx)yB xB ^ yB = (yB)(xB) = SyxB (1 + xB) ^ xB = xB(SSxB) = Sx(SSx)B = SS(SS)xB (1 + xB) * xB = B(xB)(SB(xB)) = SB(SB)(xB) = S(SSS)xB ((1 + xB) ^ xB) ^ xB = xB(SS(SS)xB) = Sx(SS(SS)x)B = SS(SS(SS))xB ((1 + xB) * xB) ^ xB = xB(S(SSS)xB) = Sx(S(SSS)x)B = SS(S(SSS))xB ((1 + xB) * xB) * xB = B(xB)(SB(SB)(xB)) = SB(SB(SB))(xB) = S(SS(SSS))xB
これにより Hello, world! は 687 bytes で表現できるようになる。
なお、これらの規則も含め、検証用に私が作成したコードはすべて GitHub に上げた。諸君は他人のコードを使うよりも、自ら実装することを好むだろうが、いくばくかの参考にはなるかもしれない。
再帰とYコンビネータ(607)
さて、Hello, world! のプログラムは、チャーチ数の生成とリストへの追加を繰り返しているだけである。繰り返しを避けることでより簡潔に記述できないだろうか。もちろん SKI コンビネータの世界でも再帰は可能だが、自分自身を呼び出すために、ちょっとした工夫が必要となる。
たとえば以下のような、リストの要素の和を計算する関数を考える。ここまで 1 行も Haskell が出てきていないので、Haskell で書いてみよう。
sum = \ x -> if null x then 0 else head x + sum (tail x)
これを SKI で表現したいが、sum の定義の中で、sum を呼び出すことができない。そこで、引数を一つ追加して定義する。
sum = \ g x -> if null x then 0 else head x + g g (tail x) -- 右辺が g ではなく g g なのがポイント!
その上で、sum sum と自分自身を引数に設定して呼び出せば、当初の関数と同様、再帰的に実行される。
再帰つながりで、どうしても Y コンビネータを使いたければ、sum の定義をちょっと変えて y sum と呼び出せば同等の振る舞いが得られる。
sum = \ g x -> if null x then 0 else head x + g (tail x) -- 右辺がちょっと変わっている。 y = (\ g -> g g) (\ y f -> f (y f)) -- Yコンビネータ
ただし、Yコンビネータは必要以上に汎用的であるため、利用するとプログラムは一般的に長くなる。そのため、それぞれの関数を個別に再帰させる方が、簡潔さという観点では優れていることが多い。
実は再帰を利用した Hello, world! についても 51b 氏が既に書いている。リンク先のプログラムではチャーチ数 30 を加える操作を共通化しているが、まずは再帰によるリストの構築までに留めると、以下のようになる。
hello = M (λ f x y . (ifnozero (y B)) (f f (cons (y B) x)) x) end-of-output main = hello <33> <100> <108> <114> <111> <119> <32> <44> <111> <108> <108> <101> <72> <0>
ここで M = λ g . g g = SII、すなわち、ものまね鳥である。
なお、この Hello, world! を Unlambda 記法で記述すると、607 bytes となる。
ショートコーディング(509)
だいぶ短くなってきたが、他に何ができるだろうか?繰り返し出てくるチャーチ数を共通化する?既に作成したチャーチ数をもとに別のチャーチ数を生成する?ここから先は様々な方法が考えられる。
今回、私はできるだけ短い 51b 数を組み合わせて必要な出力を得ることを考えた。
具体的には以下のようなプログラムで、<27> + y <73> <81> という部分が肝である。
hello = M (λ f x y . (ifnozero (y <1> <1>)) (f f (cons ((<27> + y <73> <81>) B) x)) x) end-of-output (K(K <5>)) K (SK) ... (K(K <45>)) KK
これにより 509 bytes のコードが得られた。
細かいテクニック(458)
ここからは、本質的でないが、コードを短くするために利用可能なテクニックをいくつか解説する。
- Lazy K の出力形式としてはコンビネータ記法(カッコを使う)や Unlambda 記法(適用演算子 '`' を使う)が選択できるが、引数が 1 つのときは Unlambda 記法、2 つ以上のときはコンビネータ記法を使うと、最も短く書ける。
- たとえば ss(ss) は ssss と等価である。コンビネータ記法では、後者のように書くことでカッコの分コードが短くなる。
- これは処理系に依存するが、エラー終了が可能であれば、end-of-output = K 256 よりも単純に K 等を用いた方が短い。
こうしたテクニックを利用することにより、Hello, world! のコードは最終的に 458 bytes となった。
Haskell vs F# その後
mkotha さんに直してもらったりして、Haskellのコードはだいぶ速くなりました。どうも2重ループの内側がボトルネックのようなので、そこを展開して、データ構造も変えて、UNPACKプラグマは効くので残して、正格評価を1ヶ所だけ。性能と可読性のバランスがそこそことれたかなと思ってます。C++ や F# のコードにも同じような改修を加えたら、Haskell はまた抜かれてしまいました。まぁでも、目くじら立てるほどの差でもないので、そのままにしています。
実行環境が Windows というアドバンテージがあるとはいえ、C++ も超える F# の健闘が光ります。明示的な副作用がない関数プログラミングでこれだけ速いとうれしい。コード書いてても気持ちがいいし、Microsoft でなければもっと流行っていいはず。
最終形のコードを以下に載せておきます。
ついでに Scala でも書いてみました。C++ の2倍くらいの時間でしたが、書くだけで疲れてチューニングする元気もないので、処理時間はなしでコードだけ。
Haskell のコード
Data.Vector を早く標準モジュールに採用してほしい。cabal install するくらいはいいけど、プロファイラが使えないのが痛い。cabal install するときは -p オプションを忘れずに。
import qualified Data.Vector as V import qualified Data.Vector.Unboxed as U data Node = Node { df :: {-# UNPACK #-} !Double, pu :: {-# UNPACK #-} !Double, pm :: {-# UNPACK #-} !Double, pd :: {-# UNPACK #-} !Double, iu :: {-# UNPACK #-} !Int, im :: {-# UNPACK #-} !Int, id :: {-# UNPACK #-} !Int } induceBackward :: V.Vector Node -> U.Vector Double -> U.Vector Double induceBackward nodes values = values `seq` V.convert (V.map value nodes) where next k = U.unsafeIndex values (U.length values `div` 2 + k) value (Node df pu pm pd iu im id) = (pu * next iu + pm * next im + pd * next id) * df iteration = 10000 main :: IO() main = print (maximum [value i | i <- [0..iteration-1]]) where value i = (foldr induceBackward (lastValues i) testTree) U.! 0 lastValues i = U.replicate 201 (fromIntegral i) createNode j = Node 1.0 (1.0/6.0) (2.0/3.0) (1.0/6.0) (j+1) j (j-1) testTree = map (\i -> V.fromList (map createNode [-i..i])) [0..99]
F# のコード
自分の中で No.2 言語の座に躍り出ました。はてな記法も対応してほしい。
[<Struct>] type ShortRateTreeNode = val DF : double val PU : double val PM : double val PD : double val IU : int val IM : int val ID : int new (df, pu, pm, pd, iu, im, id) = { DF = df PU = pu PM = pm PD = pd IU = iu IM = im ID = id } let induceBackward (nodes : ShortRateTreeNode []) (values : double []) : double [] = let next k = values.[values.Length / 2 + k] let value (node : ShortRateTreeNode) = (node.PU * next node.IU + node.PM * next node.IM + node.PD * next node.ID) * node.DF Array.map value nodes let ITERATION = 10000 let maturityValues i = Array.create 201 (double i) let createNode j = ShortRateTreeNode(1.0, 1.0/6.0, 2.0/3.0, 1.0/6.0, j+1, j, j-1) let testTree = Array.init 100 (fun i -> Array.map createNode [|-i..i|]) let value i = (Array.foldBack induceBackward testTree (maturityValues i)).[0] stdout.WriteLine (Array.max (Array.init ITERATION value))
C++ のコード
性能の話になると、けっきょく引き合いに出されるんですよね。
# include <vector> # include <utility> # include <memory> # include <cstdio> using namespace std; struct node { double df; double pu; double pm; double pd; int iu; int im; int id; }; auto_ptr<vector<double> > induce_backward(const vector<node> &nodes, const vector<double> &values) { const int n_nodes = nodes.size(); auto_ptr<vector<double> > ret(new vector<double>()); ret->reserve(n_nodes); const int n = values.size() / 2; for(int j = 0; j < n_nodes; j++) { const node &node = nodes[j]; double sum = (node.pu * values[n + node.iu] + node.pm * values[n + node.im] + node.pd * values[n + node.im]) * node.df; ret->push_back(sum); } return ret; } const int iteration = 10000; int main() { vector<vector<node> > test_tree; for(int i = 0; i < 100; i++) { test_tree.push_back(vector<node>()); vector<node> &nodes = test_tree.back(); for(int j = -i; j <= i; j++) { node node = struct node(); node.df = 1.0; node.pu = 1.0/6.0; node.pm = 2.0/3.0; node.pd = 1.0/6.0; node.iu = j+1; node.im = j; node.id = j-1; nodes.push_back(node); } } double maxval = 0; for(int i = 1; i <= iteration; i++) { auto_ptr<vector<double> > values(new vector<double>(201, (double)i)); for(int j = 99; j >= 0; j--) values = induce_backward(test_tree[j], *values); maxval = max(maxval, (*values)[0]); } printf("%f\n", maxval); return 0; }
Scala のコード
3年くらい前に触ったときと比べると、API が格段に充実しています。でも疲れた・・・
object ScalaBackwardInductionTest { class Node(j : Int) { val df = 1.0 val pu = 1.0 / 6.0 val pm = 2.0 / 3.0 val pd = 1.0 / 6.0 val iu = j + 1 val im = j val id = j - 1 } def induceBackward(nodes : Array[Node], values : Array[Double]) : Array[Double] = { def next(k : Int) : Double = values(values.length / 2 + k) def value (node : Node) : Double = (node.pu * next(node.iu) + node.pm * next(node.im) + node.pd * next(node.id)) * node.df return nodes.map(value) } val iteration = 10000 def main(args : Array[String]) { def createStep(i : Int) : Array[Node] = Array.range(-i, i+1).map(j => new Node(j)) val testTree : Array[Array[Node]] = Array.range(0, 99+1).map(createStep) def lastValues(i : Int) : Array[Double] = Array.fill(201)(i.toDouble) def value (i : Int) : Double = testTree.foldRight(lastValues(i))(induceBackward)(0) println((0 to iteration-1).map(value).max) } }
Haskell vs F#
VB .NET で書かれたプログラムを速くしろと言われて、Haskell と F# で書き換えたりしています。僕の目論見ではHaskellの方が速くなるはずで、そしたら『F# もいい言語ですけどね、やはり速度を求めるならネイティブ・アプリケーションでないと。』とか何とか言って、Haskell 化してしまう予定でした。だって僕は F# 初心者だし、Haskell は C++ にも負けないわけだし、Haskell が速いに決まってるじゃないですか。
ところが実際に試してみたら、F# の方が速くなってしまいました。それも2倍以上。というわけで、図らずも自分自身の Haskell 力の無さを露呈してしまったわけですが、それはともかく、Haskell が遅いとかいう汚名を着せられてしまうのは、避けなくてはなりません。
でも、ごめんなさい、僕の能力では限界です。
世の Haskeller のみなさま、なんとかこのコードを高速化あるいは、この類のコードが遅くなる理由を教えていただけないでしょうか。STUArray は面倒とか、unsafeなんちゃらは避けたいとか、無いこともないですが、まずは速くなることを確認したい。
それから F#er のみなさま、もっと速くなるよとか、こう書いた方がいいよとかあれば、忌憚なきご意見を承りたく。代入使って速いのはいいとしても、ちょっと書き方変えるだけでこれだけ結果が変わるのは意外です。
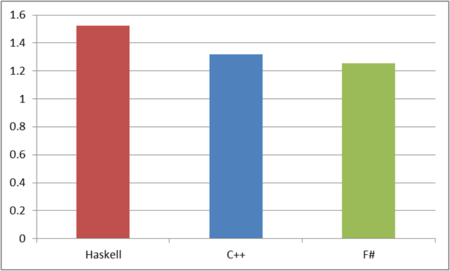
実行時間
Haskell、F# それぞれのコードの実行時間はおよそ以下の通りで、F# は何種類か書いてみました。グラフが切れてますが、F# の一番遅いやつは、一番速いやつの240倍くらいの時間がかかります。
あと構造体を使うと、F# のコードはさらに1割くらい速くなったりするのですが、気づかなかったことにしてます。

Haskell のコード
import Data.Array.Unboxed data Node = Node { df :: Double, branch :: [(Int, Double)] } induceBackward :: Array Int Node -> UArray Int Double -> UArray Int Double induceBackward nodes values = accumArray (+) 0 (bounds nodes) [(j, p * values ! k * df) | (j, Node df branch) <- assocs nodes, (k, p) <- branch] iteration = 1000 main :: IO() main = print (maximum [value i | i <- [0..iteration-1]]) where value i = foldr induceBackward (lastValues i) testTree ! 0 lastValues i = listArray (-100, 100) (repeat (fromIntegral i)) testTree = [listArray (-i, i) [Node 1.0 [(j-1, 1.0/6.0), (j, 2.0/3.0), (j+1, 1.0/6.0)] | j <- [-i..i]] | i <- [0..99]]
F# のコード
type Node = val DF : double val Branch : (int * double) [] new (df, branch) = { DF = df Branch = branch } let induceBackwardVerySlow (nodes : Node []) (values : double []) : double [] = let n = values.Length / 2 [| for node in nodes -> Array.sum [| for (k, p) in node.Branch -> p * values.[n + k] * node.DF |] |] let induceBackwardSlow (nodes : Node []) (values : double []) : double [] = let n = values.Length / 2 [| for node in nodes -> Array.sum (Array.map (fun (k, p) -> p * values.[n + k] * node.DF) node.Branch) |] let induceBackwardMedium (nodes : Node []) (values : double []) : double [] = let n = values.Length / 2 let value (node : Node) = Array.sum (Array.map (fun (k, p) -> p * values.[n + k] * node.DF) node.Branch) Array.map value nodes let induceBackwardFast (nodes : Node []) (values : double []) : double [] = let n = values.Length / 2 let arr = Array.zeroCreate nodes.Length for j in 0 .. nodes.Length-1 do let node = nodes.[j] for k in 0 .. 2 do let next = node.Branch.[k] arr.[j] <- arr.[j] + snd next * values.[n + fst next] * node.DF arr let ITERATION = 1000 let lastValues i = Array.create 201 (double i) let testTree = [| for i in 0..99 -> [| for j in -i..i -> Node(1.0, [|(j-1, 1.0/6.0); (j, 2.0/3.0); (j+1, 1.0/6.0)|]) |] |] let value i = (Array.foldBack induceBackwardFast testTree (lastValues i)).[0] stdout.WriteLine (Array.max (Array.init ITERATION value))
冪集合
2011-06-08にあったお題に挑戦。
まずはごくごく素直に。nobsunがなぜNatとか定義しているのか、よく分かっていません。
data Set = S [Set] instance Show Set where show (S xs) | null xs = "0" | otherwise = "{" ++ drop 2 (concat [", " ++ show x | x <- xs]) ++ "}" main :: IO () main = interact $ show . powerSet . read powerSet :: Int -> Set powerSet 0 = S [] powerSet n = S $ power xs where S xs = powerSet $ n-1 power :: [Set] -> [Set] power [] = [S []] power (x:xs) = [S z | S y <- power xs, z <- [y, x:y]]
ghci> powerSet 0 0 ghci> powerSet 1 {0} ghci> powerSet 2 {0, {0}} ghci> powerSet 3 {0, {0}, {{0}}, {0, {0}}}
いろいろな解があると面白そうだったので、あなごるにも出題しました。
anarchy golf - Power Set
プログラマのみなさん、ゴルファーも非ゴルファーもぜひぜひご参加を。